Implement XGBoost in Python

XGBoost is a popular supervised machine learning algorithm that can be used for a wide variety of classification and prediction tasks. It can model linear and non-linear relationships and is highly interpretable as well.

XGBoost combines the strengths of multiple decision trees, guided by strategic optimization and regularization techniques, to deliver exceptional predictive performance and interpretability. These characteristics make it a popular choice for applications across various domains like finance, healthcare, e-commerce, recommendation and ranking systems, business intelligence, time-series forecasting, and demand forecasting.

XGBoost is a very popular algorithm in data science competitions (such as the Kaggle competitions) because of its flexibility, accuracy, speed, and the support of a thriving open source community.

XGBoost stands for Extreme Gradient Boosting. Gradient boosting is an approach where new models are created that predict the residuals or errors of prior models and are then added together in ensemble to make the final prediction. It is called gradient boosting because it uses a gradient descent algorithm to minimize the loss when adding new models. Tree-based algorithms such as decision trees, bagging, or random forest solve classification and regression problems using branching decision structures. These trees are built by randomly sampling the data set. Boosting algorithms like XGBoost use the gradient descent algorithm to build trees sequentially and minimize errors without overfitting the dataset.

A critical aspect of training machine learning models is preventing your model from overfitting the training data. Data scientists are always looking to find the right balance between minimizing train error and overfitting the training data so much that the model doesn’t generalize to new data. Regularization techniques, careful hyperparameter tuning, and monitoring both training and testing errors all help develop robust models with strong, predictive performance. The hyperparameters used to tune XGBoost are a particularly important part of training.

Key XGBoost hyperparameters include:

• The number of boosting iterations, referred to as nrounds
• The learning rate (also known as eta), which is a hyperparameter that scales the contribution of each tree in the ensemble
• The maximum depth of a tree, which is a pruning parameter designed to control the overall tree depth
• gamma, which is the minimum loss reduction required to make a further partition on a leaf node of the tree.
• subsample, which is the fraction of all observations to be randomly sampled for each tree
• lambda, which is the L2 regularization term
• alpha, which is the L1 regularization term

XGBoost is customizable and has various hyperparameters that allow users to fine-tune the model for specific use cases.

In this tutorial, we will use the XGBoost Python package to train an XGBoost model on the UCI Machine Learning Repository wine datasets to make predictions on wine quality. We will then perform hyperparameter tuning to find the optimal hyperparameters for our model.

Prerequisites

You need an IBM Cloud account to create a watsonx.ai project.

Steps

Step 1. Set up your environment

While you can choose from several tools, this tutorial walks you through how to set up an IBM account to use a Jupyter Notebook. Jupyter Notebooks are widely used within data science to combine code, text, images, and data visualizations to formulate a well-formed analysis.

1. Log in to watsonx.ai using your IBM Cloud account.

2. Create a watsonx.ai project.

3. Create a Jupyter Notebook.

This step will open a Notebook environment where you can load your data set and copy the code from this tutorial to implement a binary classification task using the gradient boosting algorithm.

Step 2. Install and import relevant libraries

We'll need a few libraries for this tutorial. Make sure to import the ones below, and if they're not installed, you can resolve this with a quick pip install.

# installations
%pip install matplotlib
%pip install numpy
%pip install pandas
%pip install scikit-learn
%pip install seaborn
%pip install xgboost

#imports
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import xgboost as xgb

from sklearn.metrics import accuracy_score,confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import GridSearchCV, train_test_split

Step 3. Load the data sets

For this tutorial, we will use the wine quality datasets from the UCI Machine Learning Repository to classify wine quality using XGBoost.

1. Download the data from the UCI Machine Learning Repository.

2. Unzip the files and reformat them as .csv files.

3. Upload the two .csv files from your local system to your notebook in watsonx.ai.

4. Read the data in by selecting the </> icon in the upper right menu, and then selecting Read data.

5. Select Upload a data file.

6. Drag both your data sets over the prompt, Drop data files here or browse for files to upload. Within Selected data, select your data file (for example, winequality-red.csv) and load it as a pandas DataFrame.

7. Select Insert code to cell or the copy to clipboard icon to manually inject into your notebook. Make sure to add the sep argument to the code for the two wine data sets (for example, df_1 = pd.read_csv(body, sep = ';'))

Let's review the shape and first five rows for the white wine data set.

white_df = pd.read_csv('winequality-white.csv', sep=';')
print(white_df.shape)
white_df.head()

Output:

(4898, 12)

Let's do the same for the red wine data set.

red_df = pd.read_csv('winequality-red.csv', sep=';')
print(red_df.shape)
red_df.head()

Output:

(1599, 12)

After printing the shapes of the two dataframes, we see that the white wine data set has 4,898 instances and the red wine data set has 1,599.

Step 4. Concatenate the two data sets and conduct an exploratory data analysis

Before combining our two data sets together, let's add a column to each for a "white wine" label, where 1 designates a white wine label and 0 designates a red wine label. The white wine label not only becomes a new feature for our data set, but it is also helpful in tracking our initial two dataframes to make sure we've combined them correctly.

white_df['white_wine'] = 1
red_df['white_wine'] = 0

Next, we can combine the two data sets using the pandas function pd.concat(). Let's also check the shape of the new dataframe to make sure it adds up to the two original dataframes.

red_white_df = pd.concat([red_df,white_df])
red_white_df.shape

Output:

(6497, 13)

Before proceeding with some exploratory data analysis, let's shuffle our data so it's not starkly segmented between the red and white wine data sets and rename our dataframe wine_df.

wine_df = red_white_df.sample(frac=1).reset_index(drop = True)
wine_df.head()

Output:

Step 5. Explore the data sets

Let's check for any missing values in the combined data set.

# no missing values
wine_df.isnull().values.any()

Output:

False

We confirmed that there are no missing values in our data set. Next, let's visualize the percentage breakdown of red and white wine. Although the red and white labels won't be our target variable, it's good to check that our data sets were combined as expected.

#check that value counts match the initial white_df and red_df lengths
wine_df['white_wine'].value_counts()

Output:

white_wine
1    4898
0    1599
Name: count, dtype: int64

Let's create a pie chart to show the percentage breakdown of white vs. red wine:

wine_values = wine_df['white_wine'].value_counts().values
wine_labels = ["white wine", "red wine"]
plt.pie(wine_values,labels=wine_labels, autopct='%1.1f%%',)
plt.show()

Output:

Let's continue with visualizing our target variable, the wine quality.

fig, ax = plt.subplots()
quality_values = wine_df['quality'].value_counts().values
quality_labels = wine_df['quality'].value_counts().index
bar_colors = ['tab:red', 'tab:blue', 'tab:purple', 'tab:orange', 'tab:pink','tab:green', 'tab:brown']

ax.bar(quality_labels, quality_values, label=quality_labels, color= bar_colors)
ax.set_ylabel('Quality Count')
ax.set_xlabel('Quality Label')
ax.set_title('Quality Label Count')

plt.show()

Output:

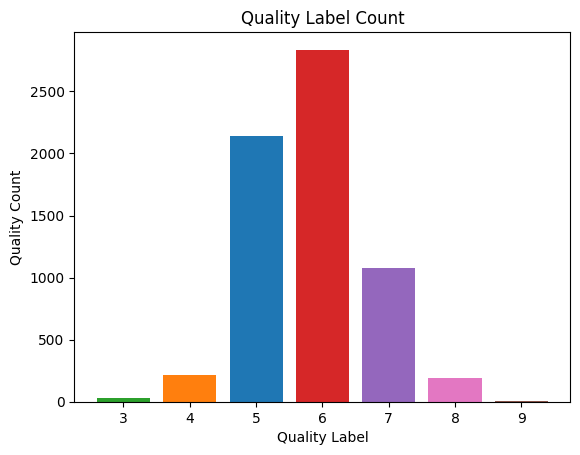
Here we can see that the label of "6" makes up a large amount of our population. And the labels of "3" and "9" happen infrequently by comparison. Having an imbalanced dataset may cause some overfitting issues where our model may learn to memorize the majority class examples (that is, our "5" and "6" labels) without capturing underlying patterns in the data for our minority classes. In order to not have such an imbalanced dataset, let's split the quality in two buckets: the first bucket contains anything "6" or higher (that is, good quality) and the second bucket contains wine of lower quality with anything labeled "5" or lower.

wine_df['good_quality'] = [0 if x < 6 else 1 for x in wine_df['quality']]
wine_df['good_quality'].value_counts(normalize=True)

Output:

good_quality
1    0.633061
0    0.366939
Name: proportion, dtype: float64

Now we see that our dataset is more balanced with a 63% good quality and 37% poor quality dataset. Although there is still a minority class, it is better represented than our initial classes of "3"s and "9"s.

Now that we have a new target variable column, we can drop the numbered quality column in favor of the good_quality column we just created.

wine_df = wine_df.drop(['quality'], axis =1)

Finally, as part of our exploratory data analysis, let's visualize the statistical correlation between our features by plotting a correlation heatmap.

mask = np.triu(np.ones_like(wine_df.corr()))

# plotting a triangle correlation heatmap
dataplot = sns.heatmap(wine_df.corr(), cmap="coolwarm",mask=mask)

Output:

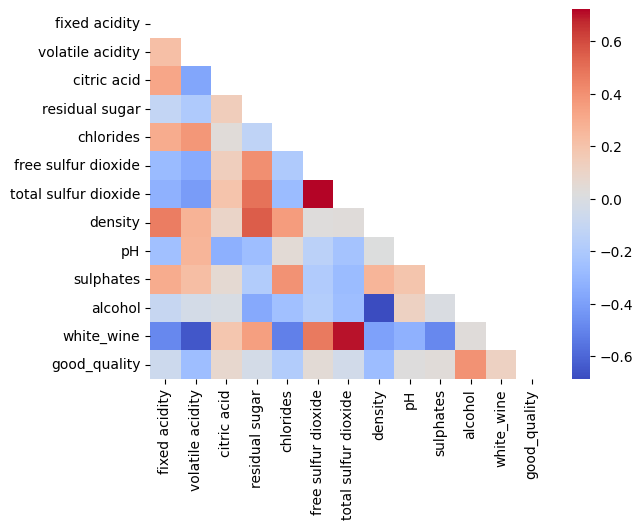
We can see some standout correlations, including a high positive correlation between total sulfur dioxide and free sulfur dioxide, as well as total sulfur dioxide having a high positive correlation with white wine. Some high negative correlations include that between alcohol and density as well as that between white wine and volatile acidity.

Step 6. Train and evaluate the model with default hyperparameters

We continue with splitting our data between a training data set and testing data set. The training data set will train our XGBoost model and the test data set will help us evaluate our model's performance. In this case, we'll set aside 30% of our data set for the test data set. We will also use the stratify parameter to ensure that our train and test data sets include the same proportion of our target variable, good_quality.

# Split data into X and y
X = wine_df.drop(columns=['good_quality'], axis=1)
y = wine_df['good_quality']

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.3, random_state=0)

Check that y_train has 63%/37% breakdown of good_quality wine:

y_train.value_counts(normalize=True)

Output:

good_quality
1    0.633165
0    0.366835
Name: proportion, dtype: float64

Check that y_test has 63%/37% breakdown of good_quality wine:

y_test.value_counts(normalize=True)

Output:

good_quality
1    0.632821
0    0.367179
Name: proportion, dtype: float64

XGBoost typically expects data to be in a DMatrix format, its internal data structure optimized for memory efficiency and training speed. Let's convert our train and test data sets to DMatrix format.

dmatrix_train = xgb.DMatrix(data=X_train, label=y_train)
dmatrix_test = xgb.DMatrix(data=X_test,label=y_test)

Once we have converted the data to the right format, we can continue with creating our baseline model. We will denote the learning objective(a.ka. our objective function), but we will not set any further parameters for now. Then we train the model using our training data set.

learning_objective = {'objective':'binary:logistic' }
model = xgb.train(params = learning_objective, dtrain= dmatrix_train)

We'll evaluate our model using our test data set using accuracy as our evaluation metric. Accuracy is a good metric to use in this case because it provides a simple and intuitive measure of how well our model is performing overall with regard to True Positives (TPs), True Negatives (TNs), False Positives (FPs) and False Negatives(FNs).

Accuracy = (TP + TN) / (TP + FP + TN + FN)

Note that we're rounding the predictions for our test set because the output predictions are in float format to denote probability, but we're expecting the output to be in 0s and 1s.

test_predictions = model.predict(dmatrix_test)
round_test_predictions = [round(p) for p in test_predictions]
accuracy_score(y_test,round_test_predictions)

Output:

0.7784615384615384

Our baseline model's accuracy is nearly 78%. Let's see if we can get higher accuracy with some hyperparameter tuning.

Step 7. Train and evaluate the model with hyperparameter tuning

GridSearchCV, which stands for "Grid Search Cross-Validation," is a technique used for hyperparameter tuning. First we set up a dictionary of parameters we want to test and then GridSearchCV systematically iterates through our dictionary to find the optimal combination which yields the best model accuracy. We will be tuning the following hyperparameters in our XGBoost model:

• Learning Rate is the rate at which the boosting algorithm learns from each iteration. A lower value of eta means slower learning, as it scales down the contribution of each tree in the ensemble.
• Gamma controls the minimum amount of loss reduction required to make a further split on a leaf node of the tree. A lower value means XGBoost stops earlier but may not find the best solution; while a higher value means XGBoost continues training longer, potentially finding better solutions, but with greater risk of overfitting.
• Max_depth represents how deeply each tree in the boosting process can grow during training. A tree's depth refers to the number of levels or splits it has from the root node to the leaf nodes. Increasing this value will make the model more complex and more likely to overfit. In XGBoost, the default max_depth is 6, which means that each tree in the model is allowed to grow to a maximum depth of 6 levels.
• Min_child_weight is used to control the minimum sum of weights required in a child (leaf) node. If the sum of the weights of the instances in a node is less than min_child_weight, then the node will not be split any further, and it will become a leaf node. By setting a non-zero value for min_child_weight, you impose a constraint on the minimum amount of data required to make further splits in the tree, encouraging simpler and more robust models. Min_child_weight curbs overfitting as its value increases. The default in the XGBoost library is 1.
• Subsample represents the fraction of the training dataset that is randomly sampled to train each tree in the ensemble. It's a form of stochastic gradient boosting that introduces randomness into the training process, helping to improve the model's robustness and reduce overfitting. Subsample should be a number between 0 and 1, where 1 means using the entire training dataset, and values less than 1 mean using a fraction of the dataset. The default value in the XGBoost library is 1. Decreasing the value from 1 helps to reduce overfitting.
• The n_estimators hyperparameter specifies the number of trees to be built in the ensemble. Each boosting round adds a new tree to the ensemble, and the model slowly learns to correct the errors made by the previous trees. N_estimators directs the complexity of the model and influences both the training time and the model's ability to generalize to unseen data. Increasing the value of n_estimators typically increases the complexity of the model, as it allows the model to capture more intricate patterns in the data. However, adding too many trees can lead to overfitting. Generally speaking, as n_estimators goes up, the learning rate should go down.
• Colsample_bytree demonstrates the percentage of features (or columns) to be randomly sampled for each tree in the ensemble during training. It's a form of feature subsampling that introduces randomness into the training process, helping to improve the model's robustness by reducing the impact of individual features and by encouraging diversity among the trees in the ensemble. Colsample_bytree should be a number between 0 and 1, where 1 means using the entire training dataset, and values less than 1 mean using a fraction of the features. The default value in the XGBoost library is 1. Decreasing the value from 1 helps to reduce overfitting.

params_grid = {
    'learning_rate': [0.01, 0.05],
    'gamma':[0, 0.01],
    'max_depth': [6, 7],
    'min_child_weight': [1, 2, 3,],
    'subsample': [0.6, 0.7,],
    'n_estimators': [400, 600, 800],
    'colsample_bytree':[0.7, 0.8],
}

Next, let's define our XGboost classifier once again to use in GridSearchCV.

classifier = xgb.XGBClassifier()

Then, we'll set up an instance of GridSearchCV with our classifier and params_grid. We'll use accuracy as our scoring method and a cv (cross validation) of 5. The cv number indicates the number of folds used in the cross-validation process. A cv of five means our dataset will be folded into 5 subsets. Each subset is then used once as a validation set while the remaining folds form the training set. We will fit the grid_classifier to our training dataset as shown below.

grid_classifier = GridSearchCV(classifier, params_grid, scoring='accuracy', cv=5)
grid_classifier.fit(X_train, y_train)

Output:

GridSearchCV(cv=5,
             estimator=XGBClassifier(base_score=None, booster=None,
                                     callbacks=None, colsample_bylevel=None,
                                     colsample_bynode=None,
                                     colsample_bytree=None, device=None,
                                     early_stopping_rounds=None,
                                     enable_categorical=False, eval_metric=None,
                                     feature_types=None, gamma=None,
                                     grow_policy=None, importance_type=None,
                                     interaction_constraints=None,
                                     learning_rate=None,...
                                     max_leaves=None, min_child_weight=None,
                                     missing=nan, monotone_constraints=None,
                                     multi_strategy=None, n_estimators=None,
                                     n_jobs=None, num_parallel_tree=None,
                                     random_state=None, ...),
             param_grid={'colsample_bytree': [0.7, 0.8], 'gamma': [0, 0.01],
                         'learning_rate': [0.01, 0.05], 'max_depth': [6, 7],
                         'min_child_weight': [1, 2, 3],
                         'n_estimators': [400, 600, 800],
                         'subsample': [0.6, 0.7]},
             scoring='accuracy')

Let's print out the best parameters found by the grid_classifier:

best_parameters = grid_classifier.best_params_
best_parameters

Output:

{'colsample_bytree': 0.7,
    'gamma': 0,
    'learning_rate': 0.05,
    'max_depth': 7,
    'min_child_weight': 3,
    'n_estimators': 800,
    'subsample': 0.7}

And finally, let's evaluate the new model with the optimal combination of parameters that GridSearchCV found. First, let's plot the confusion matrix to show TPs, TNs, FPs and FNs.

cm = confusion_matrix(y_test, grid_test_preds)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=grid_classifier.classes_)
disp.plot()
plt.show()

Output:

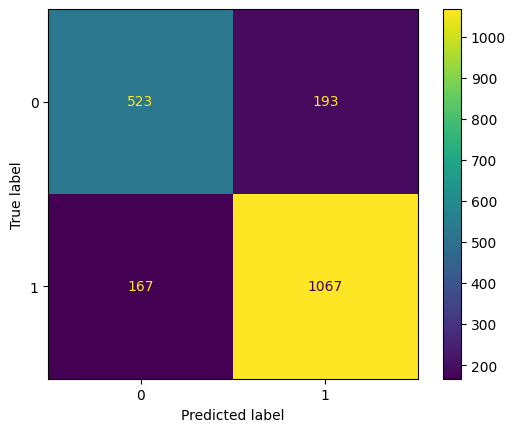
grid_test_preds = grid_classifier.predict(X_test)
grid_test_accuracy = accuracy_score(y_test, grid_test_preds)
grid_test_accuracy

Output:

0.8153846153846154

Our accuracy increased to nearly 82%. Feel free to test out some more hyperparameter options to see if you can improve upon this accuracy further.

Summary

In this tutorial, we introduced XGBoost and how it uses gradient boosting to combine the strengths of multiple decision trees for strong predictive performance and interpretability.

We’ve explored the wine data set and identified the features to use to train an XGBoost binary classification model. We learned about cross validation and grid search and implemented them using the scikit-learn library. Once the best hyperparameters were identified, we trained an XGBoost model using the best hyperparameters and compared the performance to our default hyperparameter version.

Try watsonx for free

Build an AI strategy for your business on one collaborative AI and data platform called IBM watsonx, which brings together new generative AI capabilities, powered by foundation models, and traditional machine learning into a powerful platform spanning the AI lifecycle. With watsonx.ai, you can train, validate, tune, and deploy models with ease and build AI applications in a fraction of the time with a fraction of the data.

Try watsonx.ai, the next-generation studio for AI builders.

Next steps

Explore more articles and tutorials about watsonx on IBM Developer.