Protecting AI embedding vectors by using approximate distance preserving encryption for RAG applications

Step by step, our applications are starting to integrate with AI, either using public cloud large language models (LLMs), such as OpenAI or GPT -3, or on-prem models, such as IBM Granite.

But integrating with any model has some important things you must be aware of:

• A model predicts the best possible answer, which doesn't mean it is the right answer; the model can hallucinate.
• A model generates an answer using the data that data scientists trained it on. If the data used to train the model was 5 years old, it would produce answers to your questions using outdated information. Fine-tuning or retraining the model is possible, but it requires significant time and resources.
• A model is trained with non-sensitive data, as sometimes you might have security reasons to keep the data private. Additionally, you might want to allow users to query the model with updated documentation without needing to retrain it each time.

To address these issues, you can use the well-known retrieval-augmented generation (RAG) technique to enhance the model's context, enabling it to generate more accurate answers. RAG relies on embedding vectors to find the correct text or paragraphs for each question.

In this article, I'll explain one possible vector attack that can occur when using embedding vectors and how to mitigate it.

This article assumes that you have a good knowledge of embedding vectors and how to calculate them in LangChain4j. If you need a refresher, read this introductory article, "Calculating vector embeddings for semantic search and retrieval augmented generation (RAG)."

Security Treats

There is always a risk when using sensitive data, especially the risk of a data leak exposing it to untrusted users.

When using RAG, you store three elements in the vector database:

1. The embedded vector, which is a float array representing the semantic meaning of the text.
2. Metadata information, which is configured at ingestion time.
3. The text used to calculate the vector.

Of these three elements, you probably identified two as potentially sensitive when stored in the data store. The first one is the metadata, and the second one is, of course, the text.

Suppose either of these two elements contains sensitive data, not just passwords, but also confidential information about a company or a person. In that case, the natural answer is to store this data encrypted in the data store. Nothing different from any other traditional data store.

However, there is a third part in the equation: the embedded vector, which you calculate from the text using an embedding model.

The first thought about vectors is that they do not contain sensitive data, since they are collections of numbers that reflect the semantic meaning of a word or a sentence.

And while that's true, the problem lies in the existence of reverse-embedding models, which can translate an embedding into the original text or a sufficiently close text.

So, suppose an attacker gains access to the data store and obtains the embedding vector. Since it is not encrypted, they might use a reverse-embedding model to retrieve the original text and access confidential information.

Protecting embedding vectors

Vector embeddings are just arrays of numbers, so it might feel natural to protect them with standard encryption methods. The problem with this approach is that this would break what makes them valuable, such as similarity search, recommendations, and retrieval, since all of these depend on being able to compare vectors mathematically.

Encrypting them with traditional methods is like locking them in a box: they’re safe, but you can’t measure the distances between them anymore.

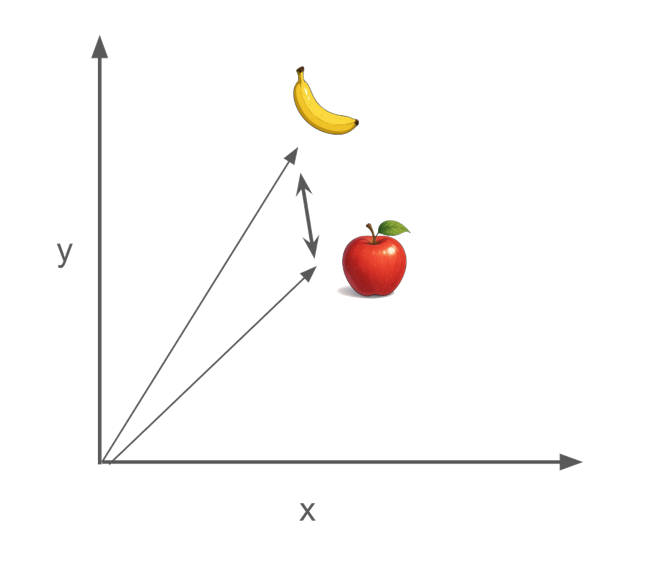
The following image shows a possible representation of two vectors in a 2D space before applying standard encryption:

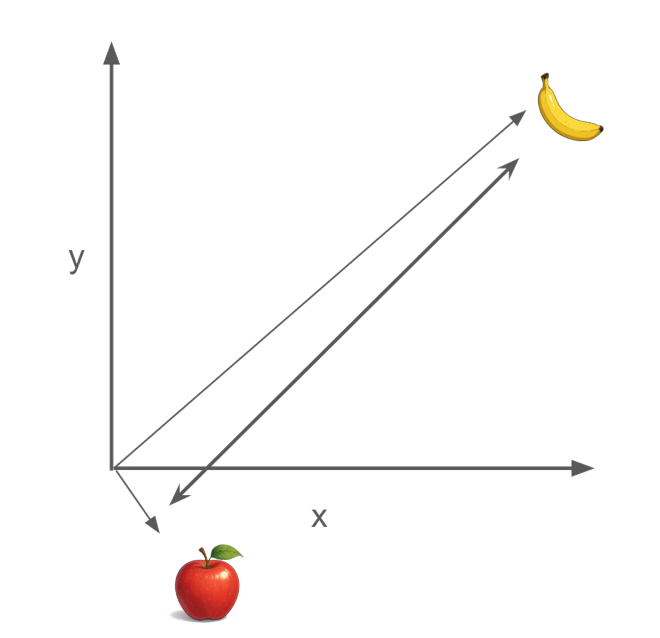
The following image shows how it might change when applying traditional encryption algorithms, not preserving the distance between the vectors:

Therefore, we cannot use traditional encryption algorithms (symmetric or asymmetric) to protect vectors. What is the solution for protecting these embeddings then?

Approximate distance-comparison-preserving symmetric encryption

Approximate distance-comparison-preserving symmetric encryption (DCPE) is a property-preserving encryption (PPE) that preserves the relative distance between encrypted vectors. This algorithm means that if two unencrypted vectors are close to each other, their encrypted versions will also be near, and vice versa.

It's important to note that this is an approximate scheme as it sacrifices a small degree of accuracy for enhanced security.

For example, after applying the DCPE algorithm, the vectors might look as shown in the following figure:

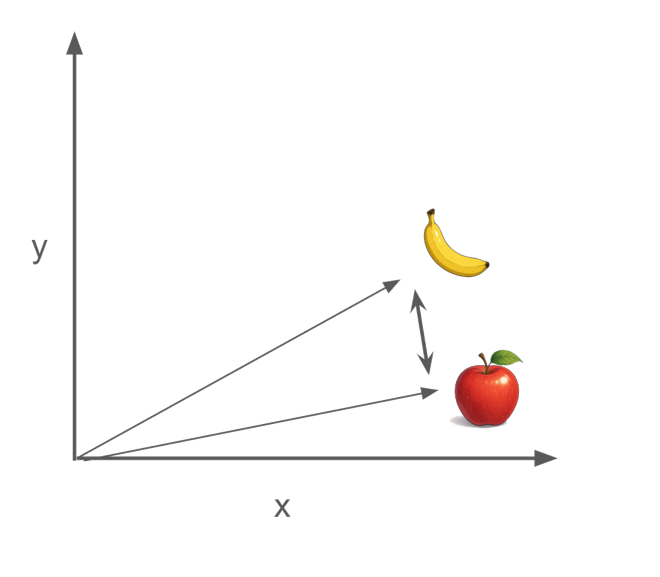
Notice that the vectors have changed their coordinates, but the distance between them is the same.

At the time of writing this article, there is no native support in vector stores for encrypting embeddings; however, some SDKs implement this algorithm.

The following figure shows the flow for protecting the vectors. From text, convert to a vector, then encrypt with the DCPE encryption algorithm.

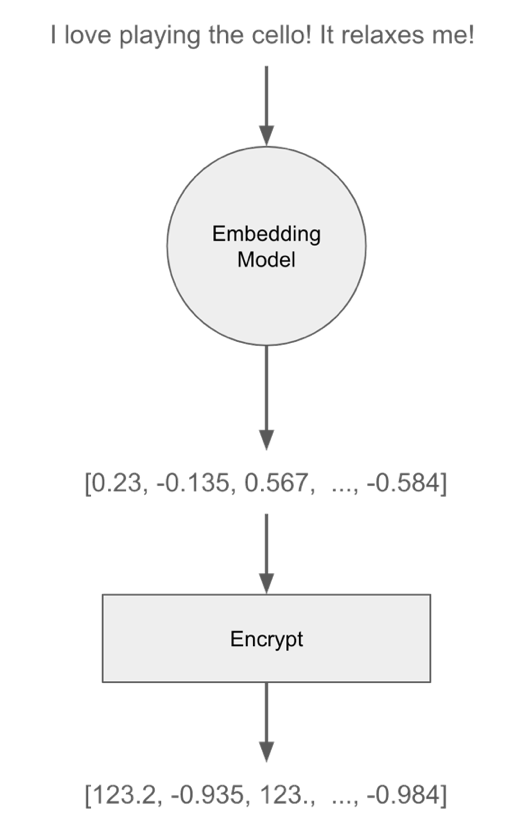
One of the most popular SDKs, and supported by Kotlin, Java, Rust, and Python, is the IronCore Labs Alloy SDK.

IronCore Labs Alloy SDK

The Alloy SDK provides a toolkit for various application-layer encryption methods, including standard, deterministic, and vector encryption.

In this article, you learn about using the Alloy SDK in Java to encrypt vectors.

We'll take the example shown in my previous vector embeddings article, "Calculating vector embeddings for semantic search and RAG," and expand it by encrypting the vectors.

Registering Ironcore Alloy Java

To use the Ironcore Alloy Java SDK, you need to register the ironcore-alloy-java dependency on Maven or Gradle.

In the case of Maven:

<dependency>
    <groupId>com.ironcorelabs</groupId>
    <artifactId>ironcore-alloy-java</artifactId>
    <version>0.13.0</version>
</dependency>

With the dependency in place, you can start using the classes to encrypt vectors.

Standalone class

To start using the SDK, you need to create an instance of com.ironcorelabs.ironcore_alloy_java.Standalone class.

This class provides methods for standard, deterministic, and vector encryption. Since we'll only use the vector encryption logic, we'll give only a key for encrypting vectors.

The key is a 32-byte cryptographically random value that you should create and store following best security practices.

For simplicity, we provide a static key hard-coded in the code. Moreover, you can configure the approximation factor, which controls how much the encryption process alters each vector. A higher factor increases security by making it harder to link encrypted vectors to their original values, but it can also reduce the accuracy of search results.

We recommend a value between 0.5 and 2.

byte[] keyBytes = "hJdwvEeg5mxTu9qWcWrljfKs1ga4MpQ9MzXgLxtlkwX//yA=".getBytes();
Float approximationFactor = 1.5f;

The next step is to create a class, com.ironcorelabs.ironcore_alloy_java.StandaloneSecret, that encapsulates the secret instance backed by the previous key. You use the StandaloneSecret class used to create the com.ironcorelabs.ironcore_alloy_java.VectorSecret instance to encrypt vectors with the given approximation factor.

The Alloy SDK supports registering multiple keys for encrypting different vectors. For example, you can use one key for encrypting all vectors generated from documents regarding employees, and another key for encrypting vectors generated from email content.

The following code generates a single vector secret with an approximation factor of 1.5, and stores it with the documents label, so you can refer to the label to set up which key to use to encrypt later. Furthermore, the vector secret contains no in-rotation secret, making the vector secret always the same value.

StandaloneSecret standaloneSecret =
                    new StandaloneSecret(1, new Secret(keyBytes));

VectorSecret vectorSecret =
                    VectorSecret.newWithScalingFactor(approximationFactor, 
                                new RotatableSecret(standaloneSecret, null));

Map<SecretPath, VectorSecret> vectorSecrets = Collections.singletonMap(
                                                    new SecretPath("documents"), vectorSecret);

The Standalone object constructor requires not only the vector encryption object, but also the standard and deterministic encryption objects. Since the example only uses the vector encryption logic, the remaining encryption objects are empty.

// Standard
StandardSecrets standardSecrets = new StandardSecrets(null, new ArrayList<>());

// Deterministic
Map<SecretPath, RotatableSecret> deterministicSecrets = new HashMap<>();

Finally, create the Standalone instance to encrypt vectors:

StandaloneConfiguration config =
            new StandaloneConfiguration(standardSecrets, deterministicSecrets, vectorSecrets);

Standalone sdk = new Standalone(config);

With the Standalone object, you can encrypt a vector. The SDK provides the class com.ironcorelabs.ironcore_alloy_java.PlaintextVector to wrap the vector to encrypt, together with the label key to use (for this example, documents as was set previously), and a derivation path to generate keys from a single root seed deterministically.

List<Float> toEncryptVector = ....;
PlaintextVector pv = new PlaintextVector(toEncryptVector,
                            new SecretPath("documents"),
                            new DerivationPath(""));

The toEncryptVector list is the embedded vector before encryption, as calculated by the embedding model.

The Alloy SDK requires you to set a tenant ID. The tenant ID is proper when encrypting vectors for different tenants, as the Alloy SDK derives a key for each tenant ID. Additionally, tenancy is important because if one tenant's key is compromised, the rest of the tenants remain safe.

The last part before executing the encrypt method is to create a tenant ID, in this case, a static one, as the example only executes code for one tenant.

AlloyMetadata metadata = AlloyMetadata.newSimple(new TenantId("tenant-1"));

And finally, using the Standalone class and the AlloyMetadata, you can encrypt the PlaintextVector.

List<Float> encryptedVector = sdk.vector()
 .encrypt(pv, metadata).get().encryptedVector();

The list contains an embedded vector that is encrypted, and you can safely store it in the vector store. If an attacker gains access to the vector and attempts to reverse it to text, they would receive random, nonsensical text instead of text reflecting the vector's intent.

The following example shows that reversing an embedding now returns a meaningless text:

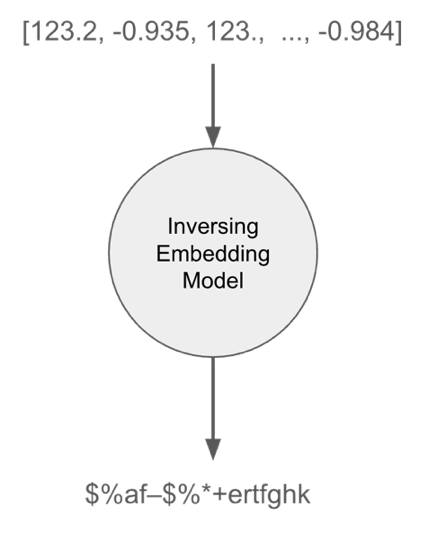
And what's even more important is keeping approximately the same distance from other vectors.

For example, encrypted vectors representing cat and kitten are:

Cat: [0.005409543, 0.02569751, -0.003617844, -0.015324947, -0.056198075, -0.02924295, 0.03488783, 0.028627029, ...]
Kitten: [0.05490739, 0.021467488, -0.06561671, -0.025412273, 0.05158478, -0.037456207, 0.011341691, -0.0339825, ...]

Using the cosine distance algorithm, the distance between the two vectors is 0.32451954.

After encrypting the previous vectors, you get something like:

Cat: [32426.11, -391970.25, -1030242.75, -358274.38, -132397.88, 218059.95, -556116.25, -518036.3, ...]
Kitten: [-395439.94, -310732.53, -1278318.1, 68877.52, -57457.23, 425827.22, -27285.766, -593491.56, ...]

Using the cosine distance with the new vectors, get a distance of 0.4095072.

So, the same distance mentioned in the post results in a slight loss; however, you are also protecting the embeddings from data leaks.

Conclusions

The first thought when using embedding vectors is that they are not reversible; it is like a one-way hash calculation. Once you obtain the numbers, it is impossible to get back to the original text. However, as you've seen in the article, this is not true, and an attacker might gain access to the embeddings and obtain a close similar value of the original text.

And this could be even worse: suppose you are converting your face into an embedding vector for authentication. An attacker can access a vector, use a reverse model to obtain an image of your face, and then use it to authenticate as a valid user.

In this article, we have only scratched the surface of embedding vectors and security. Stay tuned, though, because we'll show you how to integrate encryption with vector stores in the following article.

Next steps

If you want to learn more about Java with RAG and AI, download our book, "Applied AI for Enterprise Java Development."